Predicción en Modelos de Regresión con Series Temporales

Predicción en Modelos de Regresión con Series Temporales

Regresión: Predicción de series temporales

Resumen:

  • Cuando estimamos una regresión en R con series temporales (XTS), la predicción no se puede realizar con el comando predict.lm.
  • La soluciones pueden ser:
    • Transformar los datos en data.frame y utilizar predict.lm.
    • Utilizar el package forecast y la función forecast una vez estimado el modelo, pero siendo datos del tipo ts.

Como ejemplo estimamos el modelo CAPM de Coca-Cola y predecimos su prima de riesgo suponiendo que la prima de riesgo del mercado será del 1% para el siguiente día.

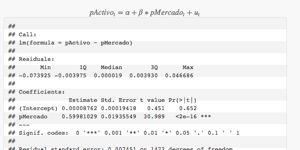
En el cuadro siguiente aparece la estimación por MCO del modelo CAPM, donde pActivo es la prima de riesgo del Activo y pMercado es la prima de riesgo del mercado:


$$pActivo_t = \alpha + \beta*pMercado_t + u_t$$

## 
## Call:
## lm(formula = pActivo ~ pMercado)
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -0.073925 -0.003975  0.000019  0.003930  0.046686 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.00008762 0.00019418   0.451    0.652    
## pMercado    0.59981029 0.01935549  30.989   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.007451 on 1472 degrees of freedom
## Multiple R-squared:  0.3948, Adjusted R-squared:  0.3944 
## F-statistic: 960.3 on 1 and 1472 DF,  p-value: < 2.2e-16

Si intentamos predecir utilizando predict.lm y xts obtenemos los valores todos los valores ajustados pero no genera la predicción: 

newdata=xts(0.01,order.by=as.Date("2015-11-11"))
predict.lm(regres,newdata)

Sin embargo, si transformamos los datos en data.frame o vectores, si que podemos: 

df=data.frame(pM=coredata(pMercado),pA=coredata(pActivo))
regres.df=lm(pA~pM,data=df)
newdata=data.frame(pM=0.01)
predict.lm(regres.df,newdata,interval="predict")
##           fit          lwr        upr
## 1 0.006085723 -0.008540464 0.02071191

La otra posibilidad es transformar los datos en ts y aplicar forecast: 

regres.ts=lm(as.ts(pActivo)~as.ts(pMercado))
forecast(regres.ts,newdata=data.frame(pMercado=0.01))
##   Point Forecast        Lo 80     Hi 80        Lo 95      Hi 95
## 1    0.006085723 -0.003474253 0.0156457 -0.008540464 0.02071191

Recomiendo la siguiente lectura del libro de Rob J. Hydman sobre regresión con series temporales:

https://www.otexts.org/fpp/4/8