Resumen:
- Cuando tenemos problemas de Autocorrelación y/o heteroscedaticidad, la estimación MCO no es válida al ser estimadores ineficientes.
-
La soluciones pueden ser:
- La estimación robusta (Newey-West) que sirve exclusivamente para realizar los contraste de hipótesis.
- Estimación por MCG (Mínimos Cuadrados Generalizados).
- En R se debe usar el package sandwich y/o forecast y/o rugarch.
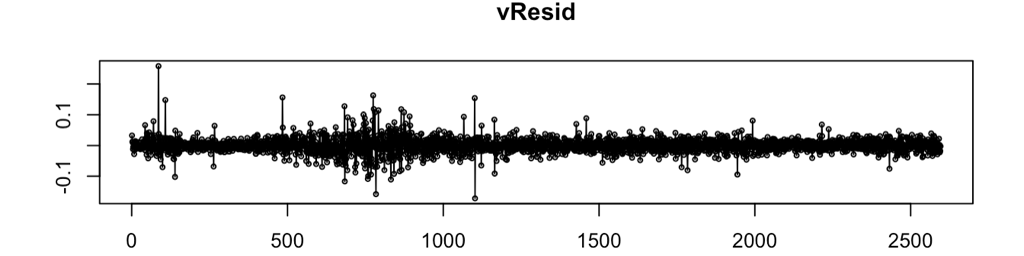
Al estimar un modelo CAPM y realizar el análisis de residuos nos encontramos con problemas de autocorrelación y/o de heteroscedasticidad. Tanto la información de la ACF y PACF (correlograma) como los contrastes (Ljung-Box) nos indican que debemos rechazar la hipótesis de ausencia de estos dos problemas.
En el cuadro siguiente aparece la estimación por MCO del modelo CAPM, donde pActivo es la prima de riesgo del Activo y pMercado es la prima de riesgo del mercado:
$$pActivo_t = \alpha + \beta*pMercado_t + u_t$$
##
## Call:
## lm(formula = pActivo ~ pMercado)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.172195 -0.010612 -0.000374 0.010352 0.257980
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.0005362 0.0004660 1.151 0.25
## pMercado 0.5902051 0.0191099 30.885 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.02374 on 2594 degrees of freedom
## Multiple R-squared: 0.2689, Adjusted R-squared: 0.2686
## F-statistic: 953.9 on 1 and 2594 DF, p-value: < 2.2e-16Al calcular la ACF y PACF de los residuos junto a los test LB, observamos que no son ruido blanco:
Análisis Residuos
</center>
##
## Box-Ljung test
##
## data: vResid
## X-squared = 50.561, df = 10, p-value = 0.0000002104##
## Box-Ljung test
##
## data: vResid
## X-squared = 67.373, df = 20, p-value = 0.000000486##
## Box-Ljung test
##
## data: vResid
## X-squared = 93.961, df = 40, p-value = 0.000003116Al calcular la ACF y PACF de los residuos al cuadrado junto a los test LB, observamos que existe autocorrelación,indicando un comportamiento ARCH:
Análisis Residuos al Cuadrado
</center>
##
## Box-Ljung test
##
## data: vResid^2
## X-squared = 216.09, df = 10, p-value < 2.2e-16##
## Box-Ljung test
##
## data: vResid^2
## X-squared = 317.62, df = 20, p-value < 2.2e-16##
## Box-Ljung test
##
## data: vResid^2
## X-squared = 559.13, df = 40, p-value < 2.2e-16Solución
Newey-West
En primer lugar podemos realizar contrastes robustos mediante la técnica de Newey-West:
- Utilizaremos el package sandwich y para realizar el contraste de hipótesis robusto. Hay que señalar que debemos introducir las variables sin formato de series temporales (XTS), para lo cuál utilizamos la función coredata().
Mas información del package se encuentra en:
https://cran.r-project.org/web/packages/sandwich/index.html
https://cran.r-project.org/web/packages/sandwich/vignettes/sandwich.pdf
library("sandwich")
coeftest(lm(coredata(pActivo)~coredata(pMercado)), vcov = NeweyWest)##
## t test of coefficients:
##
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 0.00053622 0.00044122 1.2153 0.2244
## coredata(pMercado) 0.59020508 0.03722057 15.8570 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Se puede comparar esta salida con la original y comprobar que lo único que ha cambiado son las desviaciones típicas de los estimadores y por lo tanto los test-t y sus p-valores.
Ahora se pueden realizar los contraste de significación, aunque haya autocorrelación y/o heteroscedasticidad. Pero es importante observar, que los residuos no se han corregido.
Estimación de regresión con errores ARMA
En este caso podemos utilizar el package forecast. En primer lugar, si los residuos tiene problemas de autocorrelación podemos utilizar auto.arima() para identificar el modelo y luego realizar la estimación conjunta con Arima():
library("forecast")
regres=lm(pActivo~pMercado)
vResid=resid(regres) # generamos los residuos del modelo
auto.arima(vResid)## Series: vResid
## ARIMA(2,0,1) with zero mean
##
## Coefficients:
## ar1 ar2 ma1
## -0.9036 -0.0005 0.8637
## s.e. 0.0504 0.0213 0.0464
##
## sigma^2 estimated as 0.0005583: log likelihood=6039.35
## AIC=-12070.69 AICc=-12070.67 BIC=-12047.24El modelo identificado es un ARMA(2,1). El coeficiente para el AR(2) no es significativo por lo que lo eliminaremos. Ahora podemos estimar el modelo ARMA conjuntamente con el CAPM:
\[pActivo_t = \alpha + \beta*pMercado_t + u_t\] \[u_t \sim ARMA(1,1)\]
con el parámetro order definimos el modelo ARMA , con include.mean la existencia de constante y con xreg el nombre de las variables X, en este caso pMercado
Arima(pActivo,order=c(1,0,1),include.mean = TRUE,xreg=pMercado)## Series: pActivo
## ARIMA(1,0,1) with non-zero mean
##
## Coefficients:
## ar1 ma1 intercept pM
## -0.9039 0.8645 0.0005 0.5906
## s.e. 0.0365 0.0425 0.0005 0.0190
##
## sigma^2 estimated as 0.0005583: log likelihood=6039.35
## AIC=-12068.69 AICc=-12068.67 BIC=-12039.38Ahora sería necesario continuar con el análisis de los residuos.
Estimación de regresión con errores ARCH
-
Para estimar una regresión con errores ARCH utilizaremos el package rugarch. Con esta librería no solo podemos estimar un modelo con problemas de ARCH, también con problemas de ARMA.
-
Primero debemos especificar el modelo, tanto para la media como para la varianza. Y luego estimarlo.
- Para el ejemplo, estimamos un GARCH(1,1) estándar con una distribución t-student incluimos la media y el regresor.
-
Si quisiéramos incluir un modelo ARMA , deberíamos incluir en la list la sentencia armaOrder=c(p,q).
-
Junto a la estimación, se obtiene el análisis de los residuos y sus gráficos correspondientes.
Para más información consultar:
https://cran.r-project.org/web/packages/rugarch/index.html
https://cran.r-project.org/web/packages/rugarch/vignettes/Introduction_to_the_rugarch_package.pdf
library("rugarch")## Loading required package: parallelmodelVar=list(model = "sGARCH", garchOrder = c(1, 1))
modelMean=list(armaOrder = c(1, 1), include.mean = TRUE, external.regressors = pMercado)
modelGarch=ugarchspec(variance.model=modelVar,mean.model = modelMean,distribution.model="std")
modelFit=ugarchfit(modelGarch,pActivo)
modelFit##
## *---------------------------------*
## * GARCH Model Fit *
## *---------------------------------*
##
## Conditional Variance Dynamics
## -----------------------------------
## GARCH Model : sGARCH(1,1)
## Mean Model : ARFIMA(1,0,1)
## Distribution : std
##
## Optimal Parameters
## ------------------------------------
## Estimate Std. Error t value Pr(>|t|)
## mu 0.000355 0.000302 1.1731 0.240746
## ar1 -0.723697 0.253720 -2.8523 0.004340
## ma1 0.694743 0.265452 2.6172 0.008865
## mxreg1 0.682283 0.016931 40.2971 0.000000
## omega 0.000013 0.000002 6.1658 0.000000
## alpha1 0.088097 0.008466 10.4058 0.000000
## beta1 0.891453 0.012056 73.9437 0.000000
## shape 4.065429 0.291674 13.9383 0.000000
##
## Robust Standard Errors:
## Estimate Std. Error t value Pr(>|t|)
## mu 0.000355 0.000280 1.2686 0.204596
## ar1 -0.723697 0.289161 -2.5027 0.012323
## ma1 0.694743 0.303172 2.2916 0.021930
## mxreg1 0.682283 0.030425 22.4248 0.000000
## omega 0.000013 0.000004 2.8627 0.004201
## alpha1 0.088097 0.023941 3.6798 0.000233
## beta1 0.891453 0.014617 60.9873 0.000000
## shape 4.065429 0.515659 7.8839 0.000000
##
## LogLikelihood : 6614.165
##
## Information Criteria
## ------------------------------------
##
## Akaike -5.0895
## Bayes -5.0714
## Shibata -5.0895
## Hannan-Quinn -5.0829
##
## Weighted Ljung-Box Test on Standardized Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 0.04297 0.8358
## Lag[2*(p+q)+(p+q)-1][5] 0.71875 1.0000
## Lag[4*(p+q)+(p+q)-1][9] 4.92491 0.4708
## d.o.f=2
## H0 : No serial correlation
##
## Weighted Ljung-Box Test on Standardized Squared Residuals
## ------------------------------------
## statistic p-value
## Lag[1] 2.707 0.0999
## Lag[2*(p+q)+(p+q)-1][5] 3.860 0.2720
## Lag[4*(p+q)+(p+q)-1][9] 4.648 0.4829
## d.o.f=2
##
## Weighted ARCH LM Tests
## ------------------------------------
## Statistic Shape Scale P-Value
## ARCH Lag[3] 0.6297 0.500 2.000 0.4274
## ARCH Lag[5] 1.3390 1.440 1.667 0.6357
## ARCH Lag[7] 1.5137 2.315 1.543 0.8186
##
## Nyblom stability test
## ------------------------------------
## Joint Statistic: 32.0388
## Individual Statistics:
## mu 0.3032
## ar1 0.1907
## ma1 0.2160
## mxreg1 9.8696
## omega 3.7567
## alpha1 0.7061
## beta1 0.4410
## shape 0.4609
##
## Asymptotic Critical Values (10% 5% 1%)
## Joint Statistic: 1.89 2.11 2.59
## Individual Statistic: 0.35 0.47 0.75
##
## Sign Bias Test
## ------------------------------------
## t-value prob sig
## Sign Bias 0.8671 0.38597
## Negative Sign Bias 0.6578 0.51070
## Positive Sign Bias 1.9684 0.04913 **
## Joint Effect 7.8519 0.04917 **
##
##
## Adjusted Pearson Goodness-of-Fit Test:
## ------------------------------------
## group statistic p-value(g-1)
## 1 20 45.99 0.0004976
## 2 30 51.14 0.0067844
## 3 40 62.52 0.0097966
## 4 50 72.10 0.0174879
##
##
## Elapsed time : 7.462377plot(modelFit,which="all")##
## please wait...calculating quantiles...
</body>
</html>